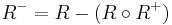Transitive reduction

In mathematics, a transitive reduction of a binary relation R on a set X is a minimal relation $R'$ on X such that the transitive closure of $R'$ is the same as the transitive closure of R. If the transitive closure of R is antisymmetric and finite, then $R'$ is unique. However, neither existence nor uniqueness of transitive reductions is guaranteed in general.

1 Example
2 Graph algorithms for transitive reduction
3 Incremental data structures
4 See also
5 References
- 5.1 Notes
- 5.2 General references
6 External links

Example

In graph theory, any binary relation R on a set X may be thought of as a directed graph (V, A), where V = X is the vertex set and A = R is the set of arcs of the graph. The transitive reduction of a graph is sometimes referred to as its minimal representation. The following image displays drawings of graphs corresponding to a non-transitive binary relation (on the left) and its transitive reduction (on the right).

The transitive reduction of a finite directed acyclic graph is unique.

The transitive reduction of a finite partially ordered set is its covering relation, which is given visual expression by means of a Hasse diagram.

Graph algorithms for transitive reduction

The transitive reduction 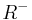$R^-$ of an acyclic relation $R$ can be computed using its transitive closure $R^%2B$ :

$R^- = R - (R \circ R^%2B)$

Here, $\circ$ denotes relation composition.

(Aho, Garey & Ullman 1972), which introduced the term in this meaning, also proves a connection between transitive closure and reduction:

they extend the computation of transitive reduction from transitive closure to deal with cycles;
they give a construction to compute a graph's transitive closure from its transitive reduction;
thus, transitive closure and transitive reduction have the same time complexity.

The tred tool in the Graphviz^[1] toolset transitively reduces a graph, using a depth-first search-based implementation.

Incremental data structures

One of the most well-studied problems in computational graph theory is that of incrementally keeping track of the transitive closure of a graph while performing a sequence of insertions and deletions of vertices and edges. In 1987, J.A. La Poutré and Jan van Leeuwen described in their well-cited Maintenance Of Transitive Closures And Transitive Reductions Of Graphs an algorithm for simultaneously keeping track of both the transitive closure and transitive reduction of a graph in this incremental fashion.^[2]

The algorithm uses

O(|E_new||V|)

time for a sequence of consecutive edge insertions and

O(|E_old||V|+|E_old|²)

time for a sequence of consecutive edge deletions, where E_old is the edge set prior to the insertions or deletions and E_new is the edge set afterwards. For acyclic graphs, the deletion algorithm requires only

O(|E_old||V|)

time. These times are still best-known, as more recent research has preferred to focus on transitive closure.

References

Notes

General references

A. Aho, M. Garey, J. Ullman (June 1972). "The Transitive Reduction of a Directed Graph". SIAM Journal on Computing 1 (2): 131–137. doi:10.1137/0201008.

External links

Mathworld: Transitive reduction